近日,复旦大学微电子学院包文中课题组,利用晶圆级的二维半导体材料MoS2,研制出了一种可以用于乘法累加运算的新型存内计算架构,拥有良好的器件耐久性,并且擦写操作简单,能够实现较长时间的多值存储能力,来实现模拟的乘加运算。从而展示了用于未来低功耗和高计算力的存算一体应用的潜力。该工作得到了复旦大学ASIC国家专用集成电路重点实验室的支持。

相关论文以题为“An In-Memory Computing Architecture Based on Two-Dimensional Semiconductors for Multiply-Accumulate Operations”发表在Nature Communication上。
.
近年来随着人工智能的不断发展,需要更多的算力来处理大量的连续矩阵运算,而矩阵运算主要包括乘法和累加运算(简称乘加运算)。在传统的冯·诺依曼计算体系结构中,存储和逻辑运算电路是分离的,运算的数据需要在内存单元和运算单元之间来回传输,而数据传输的带宽速度已经成为进一步提升其算力的瓶颈。存内计算是一种非冯·诺依曼的运算架构,它能够在数据存储的原位进行逻辑计算。存储器件的各种特性在存内计算架构里是非常重要的,包括非易失性、多值存储能力、长周期的耐久性、简单的擦除/写操作等。目前,各种不同的存储器件都已经被研究用来实现存内计算,比如非易失性存储器:阻变存储器(RRAM)、相变存储器(PCRAM)、和传统的静态随机存储器(SRAM),动态随机存取存储器(DRAM)和的闪存(FLASH)。大多数的非易失性存储器都能够实现多值存储,但是其随机性误差这会造成其在神经网络应用中识别准确率的降低。而且FLASH(~105)、RRAM(106~109)和PCRAM(106~109)都存在有限次数的刷写编程问题,并且刷写操作相对复杂,这会使得其在需要大量频繁的权重更新刷写的存算一体电路应用中受到一定程度的限制。比如FLASH就需要较高的电压来写入信息,RRAM/PCRAM则需要连续不断地电压脉冲来来调节器件电导。而易失性存储器比如和动态随机存储器(DRAM)也有在存内计算相关的研究和应用。SRAM和DRAM有着很高的刷写编程速度,并且理论上有着近乎无限次数刷写编程的能力(>1016),但是易失性存储器件需要周期性地刷新,这就很难保持不同级别的电压,再去做多值运算。所以SRAM和DRAM前的主要研究应用还主要限制在二值神经网络(BWN)领域。另外,其工艺的特殊性也导致学术界的科研团队很难灵活的调整工艺来制备存算一体器件。
具有原子级厚度的二维半导体材料为大家提供了一个研究内容丰富的科研平台,其相对简单的工艺制造流程也降低了研究存算一体器件的门槛。最近以WS2,MoS2, WSe2等过渡金属硫族化物(TMDs)为代表的一系列二维半导体材料,已经受到了台积电、三星、IMEC等权威半导体机构关注,并被认为将在下一代集成电路中发挥重要作用。目前, 二维半导体材料走向实际应用仍然有许多挑战需要克服,特别是材料的大面积可控制备及其流片工艺整合。复旦大学包文中课题组多年来聚焦于晶圆级二维半导体的集成电路应用,通过自主积累和多学科交叉合作,针对二维半导体材料的晶圆级可控生长、器件工艺集成、新型电路设计等方面系统开展了深入的系统性研究。
该工作提出了一种由两个MoS2晶体管和一个电容组成的新颖2T-1C存内计算结构。该结构实用传统的顶栅集成电路工艺制作而成,利用类似DRAM的存储单元,可以实现快速简便写入编程信息,并且理论上可以实现无限次刷写编程操作,该存内计算结构还可以实现硬件级别的权重更新、原位训练和自我学习,能够有效的避免因器件本身成对神经网络的影响,故对于在需要巨量的权重更新学习的神经网络训练中有着明显的优势。从而展示了其在用于未来低功耗高计算力的存算融合系统中的巨大潜力。
在二维材料的基础研究领域,通常使用块状晶体采用机械剥离方法来制备微米级样品,然后利用背栅来测量电学性能。而本工作中,研究者使用了晶圆级的二维MoS2材料,以及与集成电路兼容的顶栅工艺,因此更加具有实际应用意义。
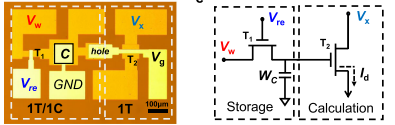
如图所示,研究者将2T-1C单元分成了存储和运算两个单元,存储单元是由1T-1C构成的DRAM结构,运算单元是另一个单独的MoS2晶体管T2。假如将多个这样的2T-1C单元按照交叉形式互连起来,其输入输出关系就可以满足矩阵运算的运算关系。
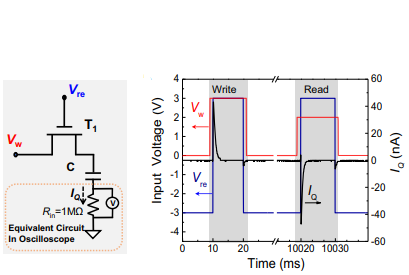
在这个2T-1C单元中,1T-1C存储模块的存储能力在存内计算中是非常重要的,图3展示了存储在电容上的电荷写入和读出的瞬态电流过程。其写入操作与DRAM类似,写入编程操作简单,并且器件理论上的写入编程的循环次数是无限的。由于较小的漏电电流是二维半导体晶体管在器件结构上存在的天然优势,所以该单元中的电容在存储不同电位的电荷之后,能够保持更长的时间,上图显示了在写入电荷后保持10s的时间,再去读取这些电荷仍然可以有效区分开来的,这就为电容的多值存储电荷提供了可行性。
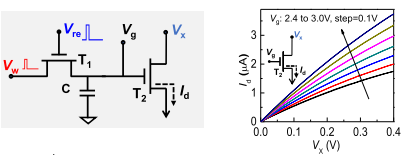
接着如图所示,就在2T-1C单元中,将1T-1C中的电容与另外一个MoS2晶体管的栅极相连通,使得电容存储的电位能够调控另外一个晶体管T2的沟道电流。图4展示了2T-1C单元在电容写入电压之后10s的周期内,T2输出端电流的变化,从中可以看出,由于1T-1C中MoS2晶体管T1的关闭状态非常完美,T2输出端电流在10s周期内大约只衰减了3%。研究者进一步测试了电容上存储不同电位的电荷,以及T2输入不同漏极电压时所对应的T2输出电流情况,结果呈现明显的电流分层,且电流之间没有出现互相干扰覆盖,这就证明了电容上不同电位的电荷保存良好,并能作为栅极电压有效地调控了T2晶体管,当它与T2本身漏极输入的电压相结合,就能够共同调控T2晶体管漏极电流的目的,这就为接下来进行多值的存储与原位运算提供了基础。
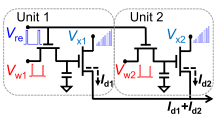
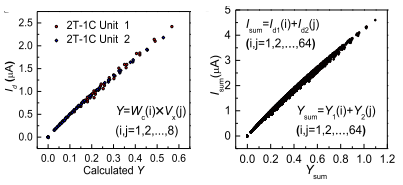
然后研究者将两个2T-1C单元连接,展示了乘法和累加(MAC)的功能,如图所示。乘法计算的实现归功于MoS2晶体管的转移特性和输出特性曲线拥有较好的线性度。所以将权重VW进行简单的变换后,和输入电压Vx进行数值相乘后,其结果Y与输出电流Id之间呈现出良好的线性的乘法关系。接下来将两个2T-1C乘法结果Y之间互相累加,其互相累加的结果Ysum与对应的电流Isum之间也呈现了良好的线性度。至此研究者验证了利用MoS2的2T-1C单元可以实现模拟电流的乘法和累加的操作(即乘加运算),其结果拥有良好的线性度,能够用来完成精确度要求一般,但是运算量较大,权重更新频繁的矩阵运算。
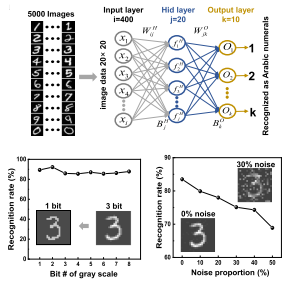
最后,研究者基于测试得到的实验数据,建立了一个拥有3层网络的全链接的神经网络仿真模型用于识别手写数字图片。在使用4000张手写数字对该神经网络训练100次以后,再使用另外的1000张手写数字图片来进行识别测试,其识别率最终能够稳定的达到90.3%左右。假如将图片中每个像素点灰度从256(8bit)位逐渐减低到2(1bit)位,发现其识别率未有明显的降低。而当在图片中加入随机噪声之后,其识别准确率随着噪声的增大而降低。研究者还发现当存储的权重数据从8bit,减少到16(4bit)位的时候,还可以保持良好的图片识别准确率。这就说明在手写数字识别这个应用场景,2个2T-1C单元即可作为神经元之间的突触连接,从而在保证识别精度的前提下计算4bit位的权重数据。
目前,由于在硬件的存储方面所面临权重次数有限,刷写操作十分的复杂等因素问题,在存算一体架构下硬件级别的神经网络训练中,往往都是采用的非原位的训练模式,即先期的训练往往都是由外部的电脑计算机软件来完成,将训练好的权重再通过转换输入到硬件的器件中,然而由于器件的非均一性、器件性能随时间的漂移、器件的损坏等等因素,会造成由软件训练好的权重转移到硬件的器件上时,无法避免的造成识别准确率的降低。本工作提出的2T-1C的存内计算结构相对比于其他存储器件实现的存内计算结构有着明显的优势, 简单快速的编程写入能够使得器件拥有快速的训练和学习能力,几乎无限次数的编程写入耐久性,保证了器件有能力处理神经网络需要巨量编程更新存储值的学习过程,这些特点使得该2T-1C结构的存算一体器件在硬件层面的神经网络的训练与学习具有很大的潜在应用价值。此外,模拟计算的电路设计,与传统的CMOS数字电路设计相比,也大大降低了电路的复杂度。
